
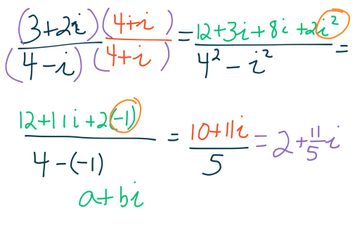
As the j-operator is commonly used to indicate the anticlockwise rotation of a vector, each successive multiplication or power of “ j “, j 2, j 3 etc, will force the vector to rotate through a fixed angle of 90 o in an anticlockwise direction as shown below. The j-operator has a value exactly equal to √ -1, so successive multiplication of “ j “, ( j x j ) will result in j having the following values of, -1, -j and +1. Real numbers can also be thought of as a complex number but with a zero imaginary part labelled j0. The only difference is in multiplication because two imaginary numbers multiplied together becomes a negative real number. The rules and laws used in mathematics for the addition or subtraction of imaginary numbers are the same as for real numbers, j2 + j4 = j6 etc. The real and imaginary parts of a complex number are abbreviated as Re(z) and Im(z), respectively.Ĭomplex numbers that are made up of real (the active component) and imaginary (the reactive component) numbers can be added, subtracted and used in exactly the same way as elementary algebra is used to analyse DC Circuits. The horizontal axis is called the “real axis” while the vertical axis is called the “imaginary axis”.
Dividing imaginary numbers plus#
Then a complex number consists of two distinct but very much related parts, a ” Real Number ” plus an ” Imaginary Number “.Ĭomplex Numbers represent points in a two dimensional complex or s-plane that are referenced to two distinct axes. Thus the letter “ j” is placed in front of a real number to signify its imaginary number operation.Įxamples of imaginary numbers are: j3, j12, j100 etc. In electrical engineering this type of number is called an “imaginary number” and to distinguish an imaginary number from a real number the letter ” j ” known commonly in electrical engineering as the j-operator, is used. As well as using normal or real numbers, Complex Numbers were introduced to allow complex equations to be solved with numbers that are the square roots of negative numbers, √ -1.

But real numbers are not the only kind of numbers we need to use especially when dealing with frequency dependent sinusoidal sources and vectors.


 0 kommentar(er)
0 kommentar(er)
